Luminescence

先日のこと。とある中学3年生から相談を受けた。イオンがよく分からない、というのである。

調べてみると、今年の中学3年生というのは、どうも悪いタイミングでこの学年になってしまったようである。この学年から、あの悪名高きゆとり教育が完全に終了し、新しい指導要領に沿ったカリキュラムに全面的に移行しているとのことで、脱・ゆとりに合わせて、イオンに関する項目が大幅に増強されているらしい。

えー、でもたしか、これって移行措置とかいうのがあるんじゃないか……と、もう少し調べてみると、移行措置の段階ではイオンの単元に入れられていなかった事項、たとえば原子の構造のようなことが、今年になってから増えているらしい。だから、この分野に関しては、去年までに増して学ぶ事項が増えているということになるらしい。

うーん。原子の構造ねえ。原子ってのは原子核と電子からできていてだな、原子核は陽子と中性子からできているんだ、これは教わったよな……と話しても、何やら寝呆けたような顔をしている。

「あー。ひょっとして、『中性子って何のためにあるんだか分かんねー』とか思ってないか？」

と聞くと、果たしてその通りだ、と言う。参ったなあ。こんなことも教えないのかよ。

「あー。陽子って、プラスの電気を帯びているんだろ？ だったら、同じプラスの電気を帯びたものが集まったら、反発する力がはたらくよな。だから、陽子だけではくっついていられないだろう？」
「はあ」
「ところが、陽子と中性子の間には、核力と呼ばれる強い力がはたらいている。これは電気的な力の数百倍の強さで、陽子と中性子を引きつけている。だから、中性子が仲立ちになることで、原子核は一体になっていられるんだ」
「……」
「この核力が、中間子という素粒子によるものだということを理論的に予測したのが湯川秀樹という人で……って、あー、本当に習ってない？」
「……はい」

こんな調子である。ゆとり教育で呆けているのは生徒だけではないということなのか？ ノーベル賞シーズンと前後してこの単元を習うという話だから、そういう話をするのが教師の仕事なんじゃないのかね？ ったく、お粗末な話である。

しかし、こんな話はまだ序の口なのであった。この子が持っていた問題集に載っている問題が、まーひどい代物だったのだ。以下に概略図を示す：

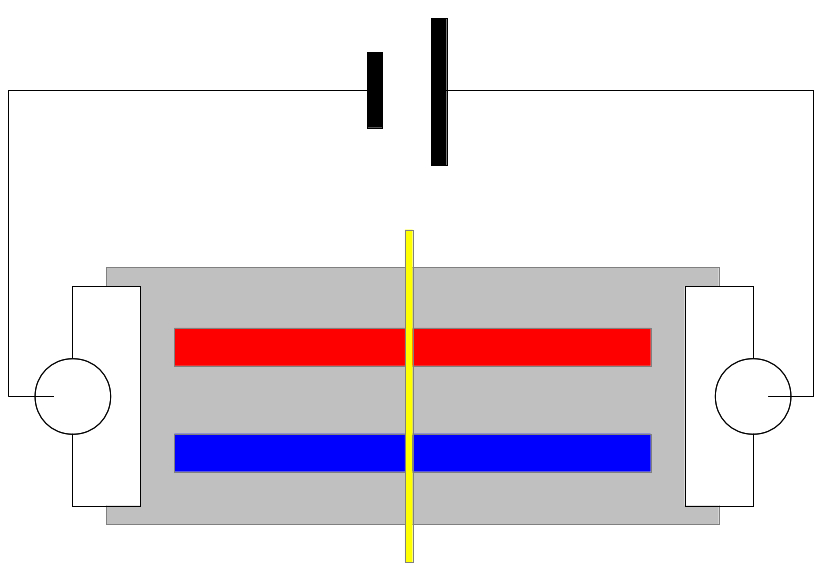
上の図は、電解質の水溶液で濡れたろ紙の上に、赤色と青色のリトマス紙が載っていて、その両端には金属製のクリップを経由して直流電圧が印加されている。2枚のリトマス紙の中央には、細く切ったろ紙（上図の黄色の部分）が置かれていて、この細く切ったろ紙には塩酸、もしくは水酸化ナトリウム水溶液がしみこませてあるらしい。この装置（とか言うのも嫌になるような代物だが）を作動させてしばらくすると、どちらのリトマス紙のどちら側（中央の黄色いラインから、右か、左か）の色が変わるか、というのが、この図で示される問題である。

「ほー。電気泳動ってわけか。でさ、君はこれ、学校の実験でやってみたことあるか？」
「はい」
「……うまくいかなかったろう？」
「そうなんですよ。全然うまくいかないんです」

どうして、中学や高校の理科の先生は、こういう愚問を生徒に出題する前に、自分で検証してみようともしないのだろうか。こんなもの、そこらの文房具と理科室に転がっているもので装置を組めば費用もかからないだろう。こんな愚問を得意気に出題している時点で、自分が無能な教師だと喧伝しているようなものなのに、馬鹿だからそういうことも理解できないのだろう。

水素イオンや水酸化物イオンというのは、たとえば DNA の構造解析などで対象とされる物質と比べて、極めて拡散し易い。だから、こんな装置を組んだって、電気泳動による移動がはっきり見える前に、下のリトマス紙にしみこんだ電解質の拡散の方が速く進行するから、こんな実験がうまくいくわけがないのである。どうしてもこれでやってみたいのなら、たとえば全体を電解質を溶かし込んだ寒天で固める、等の対策でもしない限りは、そんな絵に描いたようにうまくいく筈がないのである。

いくら無能な教師だって、塩橋というものを一度位は見たことがあるはずだ（ないとは言わせませんぜ）。なぜ塩橋は中身を寒天で固めているのか。固めなければならないのか。分かるでしょう？ ったく、どうしてこんなアホな問題のために、俺の貴重なプライベートの時間が浪費されなきゃならないんだよ。

「Thomas さん、あのー……」
「ん？ ああ、あのさ、おそらく、ゆとり教育が終わって、新しい内容で問題を作るのに、まだ先生とかも慣れていないんだろう。だから、ああ、この問題は、イオンが電気的な力によって動くということを言いたいんだな、と、無能な教師の意図を、どうか汲んでやってはもらえないだろうか」
「は、はい……」

こうやって、無能な教師は結局は生徒や受験生に甘えているようなものなのだ。いい加減にしてもらえないだろうか。

昨日、某所で猫の話になったとき「三毛猫のオスはまず生まれないし、生まれたとしても非常に稀少である」という話をしたら、そこに居る人が皆このことを知らずに一同騒然となって、逆にこちらの方が吃驚させられたのだった。

三毛猫を決める因子はいくつかあるのだが、「白猫になる遺伝子」が劣性、「茶色になる遺伝子」がヘテロ、そして「ぶちになる遺伝子」を持つ、という3条件が揃ってはじめて三毛になる、ということが分かっている。

この3因子のうち、ヘテロになることが必要な茶色の遺伝子は X 染色体の上に乗っている。いま、通常の性染色体を X, Y とし、茶色の因子が乗った X 染色体を小文字の x と書くことにする。このとき、xX で表わされるときだけ三毛になるわけだ。このように、性染色体によって性別以外の形質が遺伝するのを伴性遺伝という。

上の例では、X 染色体がふたつなければ三毛が発現しない、ということになる。つまり、オスの三毛は存在しない……ということになるのだが、自然というのはしばしば例外が存在するもので、この三毛の場合もそうである。誤解を恐れずに単純に説明すると、xX を持ち、なおかつ男性を規定する Y 染色体を持てば、その個体は三毛、かつオスということになり得るわけだ。いやそんなの無理でしょう、と思われるかもしれないが、この例で言うと xXY という染色体を持つ個体が実際に存在していて、実際に三毛のオスはこのような染色体異常を持っている。

人間の場合だとこれは「クラインフェルター症候群」の名で知られている。人間の場合、クラインフェルター症候群の発現率はおおむね 0.1 % 程度で、多くの場合、その男性は十分な生殖能力を有しない。ネコの場合、クラインフェルター症候群の発現率は 0.003 % 程度とされているので、三毛のオスがいかに希少な存在なのかは想像に難くない。そして、このようなオスの三毛は血統的に保存され得るものではない。

実は、この日記を書くにあたって、ネコの毛色に関する遺伝形態を調べてみたのだが、これが実に複雑怪奇である。実際、まだ完全にその形態が解明されたわけでもないらしい。たとえば、うちにいるネコは茶色の虎縞と白が混じっているメスなのだが、このような茶白のネコのメスはかなり珍しいらしい。俗説であるが、この柄のネコはネコとしては珍しいことにかなり社交的、というか、人懐っこいというか、と言われているのだが、たしかにその通りで、うちに宅配便などの配達がくると、このネコは玄関に出迎えに出たりする。まあそんなわけで、ネコには色々と謎が多い、というのは、日々実感させられているわけである。

大学の学部生のときに卒論で分子動力学法を用いた計算（だけじゃなくて実験もやったけどね）をして以来、何かとそういう計算に関わることがあったわけだけれど、そう言えば僕はモンテカルロ法というのを仕事に使ったことがない。

モンテカルロ法、というのは、その名から想像される通り、サイコロ→乱数を用いて行う一種のシミュレーションである。モンテカルロ法といっても非常に多岐に渡るわけだけど、僕の関わる分野でこの名が出てくるとき、そのほとんどは統計力学的事象を乱数で解くことを指す。もともとかのフォン・ノイマンが中性子の挙動を計算するのに考案した、という話だから、ある意味一番ファンダメンタルな使い方かもしれない……とか書いても、そんなの分からないよ、と思われる方が大半だと思うので、もう少し分かりやすい話を書くことにする。

まず、この図を見ていただきたい。

何の変哲もない扇形の図なのだけど、いま、この図中の正方形 OPRQ の中に点を打つことを考える。正方形 OPRQ の中に入るように点を打つと、それは扇形 OPQ の中になるときと、外になるときがある。いま、十分に数多く、てんでバラバラになるように点を打ったとして、全体の点の数を N、扇形 OPQ の中に打たれた点の数を n とすると、点の数は打たれる点の範囲の面積に比例するので、

N : n = (1 × 1) : (1 × 1 × π ÷ 4)

π = 4 n / N

いやだから何なんだ、と思われるかもしれないが、要するに、一様乱数 x, y（ただし x, y = [0,1]）で定められる点 (x, y) を十分大きな数である N 個打ったとき、

x² + y² ≦ 1

これは数学的には何をやっていることになるのか、というと、円の面積を積分で求め、そこから円周率を算出する、という操作である。円の場合はこんなことをする必要はないわけだけど、解析的に積分するのが難しいような関数であっても、この方法で積分することができるわけで、これをモンテカルロ積分という。積分区間で乱数で点を打ち、それが積分される領域に属するかどうか検定することで、面積や体積を求めることができるわけだ。

しかし、完全に一様、かつバラバラな乱数というものがあるのかどうか、ということが問題になるわけだ。たとえば、僕等が使うプログラミング言語…… C とか Fortran とか、最近だったら Java とか C# とか……には大抵「乱数を生成する関数」というのがある。もっと卑近な例で言うなら Excel にだってあるわけだが、これを使ってこのような計算をして、果たして円周率が計算できるのか、というと、実はできない。これは計算機の能力の問題ではなくて、計算機で「良質な」乱数を得ることが難しい、ということを反映している。

現在使われている乱数生成法で最も良質、かつ高速なものとされているMersenne Twisterを用いてこの計算を行ってみると、N = 10⁹ の場合で、3.1416112599999999 という計算結果を得た。なんと、10億個も乱数のペアを計算して、せいぜい4、5桁の精度でしか円周率が計算できない、ということになるわけだ。

……とか書くと、あたかも Mersenne Twister に問題があるみたいに思われそうだけど、そもそもこうやって計算を行った場合の「分解能」を考えると、これはおおむね N の平方根と同じ桁数ということになるから、4〜5桁、ということで、上の結果はちゃんとこの分解能の範囲内で妥当な結果を出せている。

もちろん、僕はこのような計算を、円周率を求めるためにしているわけではない。そもそもこの円の求積法による計算は乱数を使う必要などない。等間隔に細かく、規則的に点を打ったって計算はできる（し、その方が桁数の制限の中ではより妥当な結果を返すだろう）のだが、こういう計算で既知の値に対してどのような計算結果が得られるか、で、乱数の質を判定することができるわけで、その判定のためにこういう計算をすることがある、というわけである。また、Mersenne Twister の名誉のためにもフォローしておくけれど、Mersenne Twister は現存する乱数の中では非常に素性がいいものとされている。素性のいいものを活かすも殺すも、使う側の理解度と使い方にかかっている、というわけなので、どうか誤解されないように。

少し前のことになるけれど、大塚食品が OS-1 という商品を出した。これは、医学的に体内に水分が取り込まれ易いように調製されたいわゆる経口補水液といわれるものである。

標準的なレシピは：

• 水 1リットル
• 砂糖 40グラム
• 食塩 3グラム

• 水 1リットル
• 砂糖 30 cc（24 グラム）
• 食塩 2.5 cc（2.5 グラム）

このレシピにある通り、ORS のミソは、水だけではなく（水＋塩分＋糖分）という配合になっているところだ。水だけ、あるいは、水と塩だけの場合と比較して、糖分が加わる方が吸収効率は高くなるのである。

恥を忍んで告白するが、昨日、風呂に入っていたときに軽い熱中症になってしまった。一般に、熱中症の自覚症状としては、

• めまい
• 頭痛
• 吐き気
• 気分が悪くなる

慌てて風呂を出て、うろ覚えのレシピで ORS を調合して、ガブリと飲むと……ま、不味い……塩の量を間違えて倍にしていたのだった。せっかく棚の中からクエン酸を探し出して、震える手でキッチンメーターを使って秤量したのに……

とりあえず「水1リットル、塩小匙半分、砂糖大匙2」と覚えておけば、ご家族や御自身のもしものときに役立つので、この機会に覚えておきましょう……誰かさんみたいに塩を倍入れないためにも。あと、本当はブドウ糖の方が吸収がいいと思うので、先の OS-1 を買い置きされた方がよりいいと思う。