Luminescence

何かと質問を受けることの多い今日この頃なわけだが、今度は高校生の数学の質問だった。

| x - 2 | + | x - 4 | = x を解け。

なんでも、数学 I という科目では、絶対値のついた方程式がよく出題されるらしい。うーん、丁寧に場合分けをするか、グラフでも書くかするかすればいいんじゃないの？ と言うと、意味が分からぬらしくきょとんとした顔をされる。うーん……

| x - 2 | =

x ≥ 2 → x - 2

x < 2 → 2 - x

| x - 4 | =

x ≥ 4 → x - 4

x < 4 → 4 - x

だから、

| x - 2 | + | x - 4 | = x

x < 2 → (2 - x) + (4 - x) = x ...(1)

2 ≤ x ≤ 4 → (x - 2) + (4 - x) = x ...(2)

x > 4 → (x - 2) + (x - 4) = x ...(3)

と書くことができる。これらを解くと、

(1) x < 2 →

(2 - x) + (4 - x) = x

3 x = 6

x = 2 ……これは x < 2 に反するので棄却。

(2) 2 ≤ x ≤ 4 →

(x - 2) + (4 - x) = x

x = 2 ……これは 2 ≤ x ≤ 4 に属するので解。

(3) x > 4 →

(x - 2) + (x - 4) = x

x = 6 ……これは x > 4 に属するので解。

よって解は x = 2, 6 となる……と紙に書いてみるが、「ん？ ん？」となってパニクってしまう。うーむ。ではこれならどうよ。

「y = |x - 2| ってのをグラフに書くと、y = x - 2 を 書いて、x 軸の下側を上側に折り返したものになるよな。だったら、このグラフの黒線になるだろう？」
「はい」
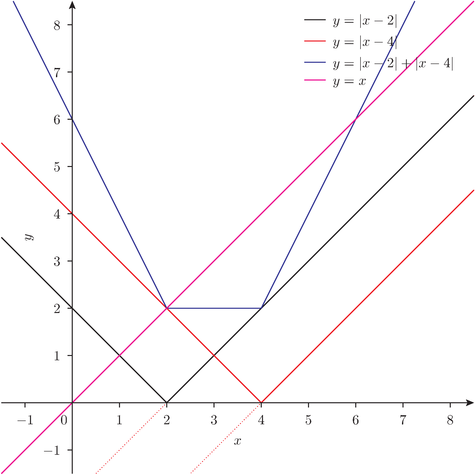
「次。y = |x - 4| ってのをグラフに書くと、y = x - 4 を 書いて、x 軸の下側を上側に折り返したものになるよな。だったら、このグラフの赤線になるだろう？」
「はい」
「では、グラフの黒線と赤線の y の値を足したものを考える。そうすると、x < 2 では傾き -2、x > 4 では傾き2、そしてその間では傾き 0 の直線になる……このグラフの青線のように。これが、y = | x - 2 | + | x - 4 |、だよな」
「はい」
「| x - 2 | + | x - 4 | = x の解、ってのは、この青線と、y = x の交わる点だよな。交わってるところでは | x - 2 | + | x - 4 | = x なんだから」
「……はい」
「じゃあ、y = x をピンクの線で書いて……交点の x 値を読めば、それが答だな。えーと…… x = 2, 6。これでいいよね？」

彼はまた「ん？ ん？」と言いながらグラフを見直し始めたが……あー、分かりました、と呟いた。

まあ、いきなりこれに慣れるのも難しいか、ということで、次の問題をこの方法で解いてみてもらう。

| | x - 4 | - 3 | = 2 を解け。

うーん……となる彼に、
「まず、y = | x - 4 | のグラフを書いてみようか」

「……こ、こうですか」
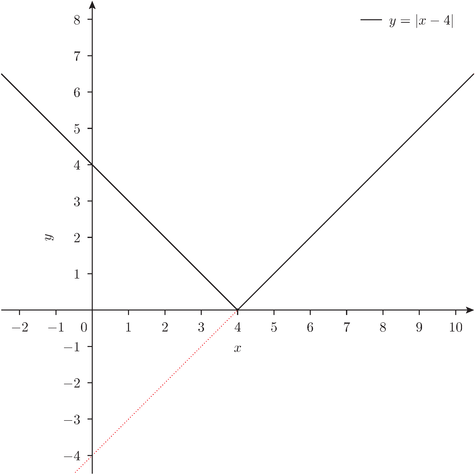
「うん。じゃあ、それを基に y = | x - 4 | - 3 のグラフを書くとどうなる？」
「マイナス 3 って……どうしたらいいんですか？」
「3 引くんだから、3 下にずらしたらいいんだろう」
「……こうだよな。で、この | x - 4 | - 3 の絶対値ってことは、どうなる？」
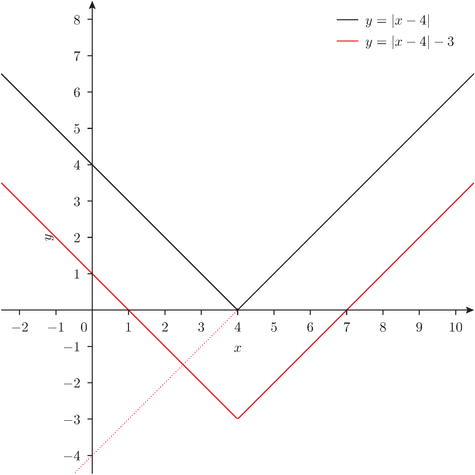
「折り返すんですよね……」
「……こうですか？」
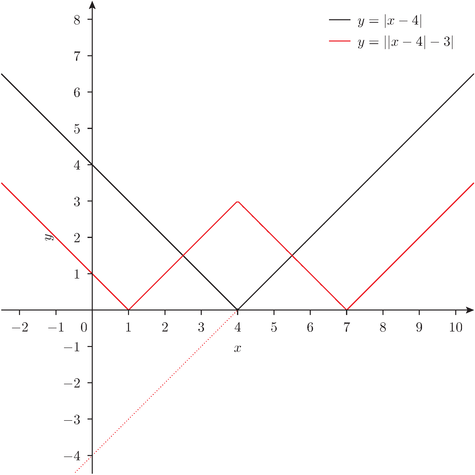
「そう。これで、y = | | x - 4 | - 3 | が書けたわけだ。で、これが 2 になるとき、ということは、y = 2 の線を引けば……」
「……こうですか？」
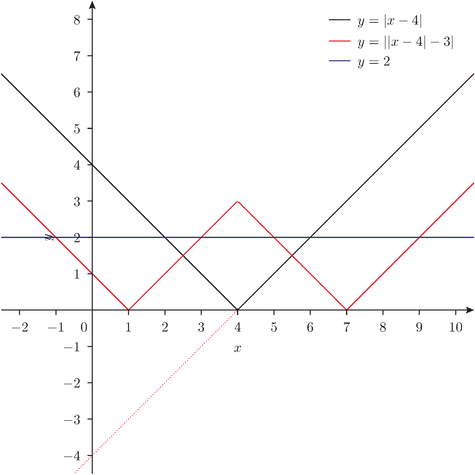
「そうそう。この赤線と青線の交点の x の値が解、ということになるわけだ」

彼は目を丸くして、しばしグラフに見入っていたのだった。

僕は、式だけでこのような式を解くときでも、このようなグラフをラフに書くのが習慣になっている。こうやれば見落しを防げるし、思いもしなかったことに気付くこともあるからだ。そして、高校生的には、このグラフにはもうひとつの大きな利点がある。解答用紙にこのグラフをちゃんと書けば、「上図より x = 2, 6 である」とか、「上図より x = -1, 3, 5, 9 である」とか書くだけで、このグラフ自体がそのまま解答になってしまうのだ。これは便利である。

このような視覚的理解というのは、一見、厳密な数学的理解を満たさないように見えるかもしれない。しかし、言葉を連ねるより図をひとつ書く方が、書くのも簡単だし、伝わる情報も多い。このようなセンスは理系には大事なものなのだが……もっと、脳ミソの力を抜かなきゃならないんだろうなあ、この子は。